Implicit solvation using a generalized finite-difference approach in CRYSTAL: implementation and res

Journal of Chemical Theory and Computation 2018

DOI: 10.1021/acs.jctc.8b00762

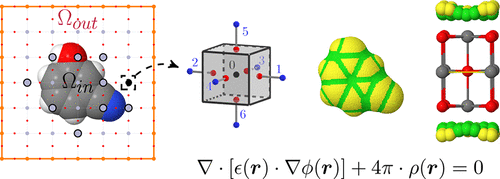
We present the implementation of an implicit solvation model in the CRYSTAL code. The solvation energy is separated into two components: the electrostatic contribution arising from a self-consistent reaction field treatment obtained within a generalized finite-difference Poisson model, augmented by a nonelectrostatic contribution proportional to the solvent-accessible surface area of the solute. A discontinuous dielectric boundary is used, along with a solvent-excluded surface built from interlocking atom-centered spheres on which apparent surface point charges are mapped. The procedure is general and can be performed at both the Hartree–Fock and density functional theory levels, with pure or hybrid functionals, for systems periodic in 0, 1, and 2 directions, that is, for isolated molecules and extended polymers and surfaces. The Poisson equation resolution and apparent surface charge formalism is first validated on model analytical test cases. The good agreement obtained on solvation free energies is further confirmed by calculations performed on a large test set of 501 neutral molecules, for which a mean unsigned error of 1.3 kcal/mol is obtained when compared to the available experimental data. Importantly, the self-consistent reaction field procedure converges well for all molecules tested. This is further verified for all polymers and surfaces considered. In particular, for periodic systems, results obtained on an infinite glycine chain and on the wettability parameters of SiO2 surfaces are in good agreement with previously published data. The size extensivity of the energetic terms involved in the electrostatic contribution to the solvation energy is also well verified. These encouraging results constitute a first step to take into account complex environments in the CRYSTAL code, potentially allowing for a more accurate modeling of complex processes for both periodic and nonperiodic systems.